Calculus to produce best 2 orthographic projections (2D previews) -- of 3D meshes -- such that you can use projections to do reconstruction of meshes
Anthropic’s Assistant (+ own research to do manual insertion of URLs to more resources) is source of responses.
Q: https://wikipedia.org/wiki/3D_projection
Here are the key points about 3D projection based on the Wikipedia article:
1. Overview:
- 3D projection is a design technique used to display a 3D object on a 2D surface.
- It relies on visual perspective and aspect analysis to project a 3D object onto a 2D plane.
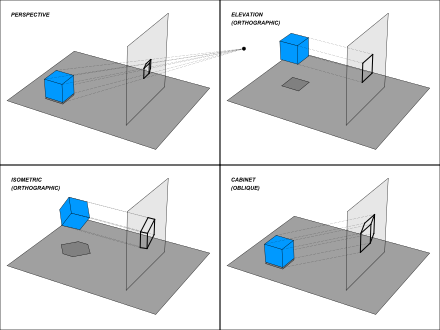
- 3D projections use the object's basic shape to create a map of points that are connected to create a 2D visual representation.
- 3D projections are commonly used in engineering, drafting, and computer graphics.
- In parallel projection, the lines of sight from the object to the projection plane are parallel.
- Parallel lines in 3D space remain parallel in the 2D projection.
- Parallel projection corresponds to a perspective projection with an infinite focal length.
- Special cases of parallel projection include orthographic and oblique projection.
- Orthographic projection is a type of parallel projection where the viewing direction is perpendicular to the projection plane.
- It is a 2D representation of a 3D object, commonly used in technical drawings.
- The mathematical transformation for orthographic projection parallel to the y-axis is provided.
- Oblique projection is a type of parallel projection where the viewing direction is not perpendicular to the projection plane.
- Specific types of oblique projection include cavalier, cabinet, and military projection.
- Perspective projection involves projecting the 3D object onto the 2D plane using a finite viewpoint and focal length.
- This results in the appearance of depth and distance, as objects further away appear smaller.
- Weak perspective projection is a variant of perspective projection.
6. Diagrams are provided to illustrate the different types of 3D projections.
Q: Formula to use *3D projection* to produce 2 2D images which capture as much of a complex 3D object as possible? (As opposed to a 3D model viewer whose preview is always a 2D head-on preview + a 2D fixed-rotation preview)
To produce two 2D images that capture as much of a complex 3D object as possible, you can use a technique called multiview projection, which is a type of parallel projection.
The key steps are:
1. Determine the three principal orthographic views:
- Front view (or elevation)
- Top view (or plan)
- Side view (or profile)
2. Apply the orthographic projection formula to each principal view:
Front view (elevation):
```
x' = x
y' = y
z' = 0
```
Top view (plan):
```
x' = x
y' = 0
z' = z
```
Side view (profile):
```
x' = 0
y' = y
z' = z
```
Where (x, y, z) are the coordinates of the 3D object, and (x', y', z') are the coordinates of the 2D projection.
3. Arrange the three orthographic views in a standardized layout, typically with the front view on the left, the top view above, and the side view on the right.
This multiview projection technique allows you to capture the full 3D shape of a complex object using just three 2D views, without requiring a 3D model viewer. The three views together provide enough information to reconstruct the original 3D geometry.
The advantage of this approach over a 3D model viewer's fixed 2D previews is that the multiview projection captures the object from multiple essential perspectives, giving a more comprehensive representation of the 3D form.
Q: Your example is 3 fixed rotations (or a head-on view plus 2 fixed rotations) to produce 3 previews, which ignores the geometric attributes of the object. Does a formula exist which processes the geometric attributes to determine the best transformations to produce 2 previews which humans can use to deduce as much of the geometric attributes as possible?
You're right, the three-view orthographic projection I described earlier is a bit limited, as it uses a fixed set of views regardless of the specific geometric attributes of the 3D object.
To determine the optimal two 2D preview images that can capture more of the geometric attributes of a complex 3D object, we can use a technique called principal component analysis (PCA).
The general formula would be:
1. Perform PCA on the 3D object's vertex data to determine the three principal axes of the object.
2. Use the first two principal axes to define the two projection planes for the 2D previews.
The steps would be:
1. Collect the 3D vertex data of the object into a matrix X, where each row represents the x, y, z coordinates of a vertex.
2. Compute the covariance matrix C of X:
```
C = (X - mean(X))' * (X - mean(X)) / (n-1)
```
where n is the number of vertices.
3. Find the eigenvectors and eigenvalues of the covariance matrix C using SVD (Singular Value Decomposition):
```
[U, S, V] = svd(C)
```
The columns of U are the principal axes (eigenvectors) of the 3D object.
4. Use the first two columns of U to define the two projection planes:
- Projection plane 1: normal vector = U(:,1)
- Projection plane 2: normal vector = U(:,2)
5. Apply orthographic projection onto these two planes to generate the two 2D preview images.
The advantage of this approach is that it determines the two most informative 2D views based on the object's actual geometric shape, rather than using a fixed set of views. This can provide a more comprehensive representation of the 3D object's form, allowing users to better deduce its geometric attributes.
Resources have to do with rasterization, which has uses with: